spectral spaces; snark

(Update 12/24: Unfortunately the argument below doesn’t work as written. I overlooked the following detail in my “proof” that $X^{wl} \to X$ is open: if $S \to S'$ is a surjective continuous map of finite $T_0$ spaces, it’s not necessarily true that $S^Z \to S'^Z$ is surjective. For instance, if $S'= \{ \eta \rightsquigarrow s \}$ is the spectrum of a DVR and $S=\{ \eta, s \}$ is $S'$ equipped with the discrete topology, then $S'^Z$ has three points but $S=S^Z$ has two.

For the argument below to work, it would be enough to know that for any open subset $V \subset X^{wl}$ , its image in $X$ contains an open subset. Is this true?

In any case, the Corollary is still true, although by a totally different argument.)

*****

I spent about six hours yesterday and today proving the following thing.

Lemma. Let $X$ be a spectral space, and let $Z$ be a closed generalizing nowhere-dense subset of $X$ . Then $Z$ is nowhere-dense for the constructible topology on $X$ , i.e. $Z$ doesn’t contain any nonempty constructible subset of $X$ .

This has the following concrete consequence, which is what I really needed.

Corollary. Let $(A,A^+)$ be some Tate-Huber pair with adic spectrum $X=\mathrm{Spa}(A,A^+)$ , and let $Z \subset X$ be a Zariski-closed nowhere-dense subset. Suppose $U_1$ and $U_2$ are quasicompact open subsets of $X$ such that $U_1 \cap (X - Z) = U_2 \cap (X - Z)$ . Then $U_1 = U_2$ .

Proof of Corollary. We need to check that $V= (U_1 \cup U_2 ) - (U_1 \cap U_2)$ is empty. But $V$ is a constructible subset of $X$ contained in $Z$ , so this is immediate from the lemma.

Amusingly, even though this corollary is pretty down-to-earth, I only managed to prove it by proving the lemma, and I only managed to prove the lemma by exploiting the structure of the w-localization $X^{wl}$ of $X$ . Is there a more direct approach? Am I missing something obvious?

(Sketch of actual argument: the profinite set of closed points $X^{wl}_{c}$ maps homeomorphically onto $X$ equipped with the constructible topology, so if $V \subset X$ is constructible it is clopen when viewed as a subset of $X^{wl}_{c}$ . The key point is then to check that $Z$ is nowhere-dense when viewed as a subset of $X^{wl}_c$ . This can be done, using that the natural surjection $t: X^{wl} \to X$ is open and that $t^{-1}(Z)$ (which is then closed, generalizing and nowhere-dense in $X^{wl}$ , the last point by openness of $t$ ) is the preimage of its image in $\pi_0(X^{wl}) \cong X^{wl}_c$ .

The openness of $t$ doesn’t seem to be stated in the literature, but it can be deduced from the proof of Lemma 2.1.10 in Bhatt-Scholze, using the fact that it’s obviously true for finite $T_0$ spaces.)

You may have noticed that RIMS is hosting a series of four workshops next year under the umbrella of a “RIMS Research Project” entitled Expanding Horizons of Inter-universal Teichmuller Theory. The first of the workshops looks pretty reasonable, the other three not so much. In case you’re wondering (as I did) how much money RIMS is ponying up for this, it seems to be capped at 5 million yen, or about $41k (according to e.g. this document). This doesn’t seem like very much money to support four workshops; I guess some funding is also coming from that infamous EPSRC grant.

Anyway, when you’re inside a black hole, your horizons might seem quite expansive indeed, but I doubt you’ll have much luck convincing others to join you.

3 thoughts on “spectral spaces; snark”

That £2.3M 6-year EPSRC grant which, presumably, you are alluding to only has 16 mths left to run, so they may well be looking for ways to spend it. Whether they can demonstrate a corresponding return on investment may be more of an open question, now that any enthusiasm for IUT which may have existed has well and truly evaporated.

LikeLike

“by a totally different argument” – could you explain it?

LikeLike

arithmetica says:

January 14, 2020 at 10:46 am

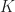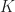OK, I have to admit that didn’t think through all the details, but if $A$ contains a nonarchimedean field $K$ then by an approximation argument I think you can reduce to the case where $A$ is a tft $K$ -algebra, where it is definitely true (by a “trivial” argument). Feel free to email me if you want to discuss this in more detail.

LikeLike

Reply

	Sorry if I am wrong,… on When is it supercuspidal?
	totally disconnected on When is it supercuspidal?
	Sorry I could be wro… on When is it supercuspidal?
	vigneras on Questions on mod-p representat…
	totally disconnected on p-adic Langlands is weird

Share this:

Like this:

Related

3 thoughts on “spectral spaces; snark”

Leave a Reply Cancel reply