Let 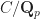 be a complete algebraically closed nonarchimedean field extension, and let
be a complete algebraically closed nonarchimedean field extension, and let 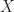 be any proper rigid space over
be any proper rigid space over  . Let
. Let  be any
be any 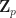 -local system on
-local system on 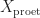 . By the main results in Scholze’s p-adic Hodge theory paper, the pro-etale cohomology groups
. By the main results in Scholze’s p-adic Hodge theory paper, the pro-etale cohomology groups  are always finitely generated
are always finitely generated 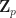 -modules. It also seems likely that Poincare duality holds in this setting (and maybe someone has proved this?).
-modules. It also seems likely that Poincare duality holds in this setting (and maybe someone has proved this?).
Suppose instead that we’re given a 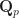 -local system
-local system  . By analogy, one might guess that the cohomology groups
. By analogy, one might guess that the cohomology groups 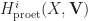 are always finitely generated
are always finitely generated 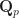 -vector spaces. Indeed, this (and more) was claimed as a theorem by Kedlaya-Liu in a 2016 preprint. However, it is false. The goal of this post is to work out an explicit counterexample.
-vector spaces. Indeed, this (and more) was claimed as a theorem by Kedlaya-Liu in a 2016 preprint. However, it is false. The goal of this post is to work out an explicit counterexample.
So, consider  as a rigid space over
as a rigid space over  . This is the target of the Gross-Hopkins period map
. This is the target of the Gross-Hopkins period map  , where
, where  is (the rigid generic fiber of the base change to
is (the rigid generic fiber of the base change to 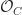 of) the Lubin-Tate deformation space of some fixed connected p-divisible group
of) the Lubin-Tate deformation space of some fixed connected p-divisible group  of dimension 1 and height 2. The rational p-adic Tate module of the universal p-divisible group
of dimension 1 and height 2. The rational p-adic Tate module of the universal p-divisible group 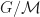 descends along
descends along 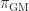 to a rank two
to a rank two 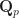 local system
local system  on
on 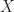 .
.
Theorem. Maintain the above setup. Then
i. For any  the group
the group  is zero.
is zero.
ii. The group  is a Banach-Colmez space over
is a Banach-Colmez space over  of Dimension
of Dimension  .
.
iii. The group 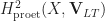 is a Banach-Colmez space over
is a Banach-Colmez space over  of Dimension
of Dimension  .
.
Recall that a Banach-Colmez space is a special kind of topological  -vector space (really it’s a functor valued in such things, but I’ll be a little sloppy about this point). Morally, it’s something like a finite-dimensional
-vector space (really it’s a functor valued in such things, but I’ll be a little sloppy about this point). Morally, it’s something like a finite-dimensional  -vector space defined up to a finite-dimensional
-vector space defined up to a finite-dimensional  -vector space. In particular, any such space has a well-defined Dimension, which is a pair in
-vector space. In particular, any such space has a well-defined Dimension, which is a pair in  whose entries record the
whose entries record the  -dimension and the
-dimension and the 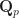 -dimension of the space, respectively. So for example the space
-dimension of the space, respectively. So for example the space 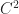 has Dimension
has Dimension 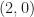 , and the space
, and the space 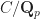 has Dimension
has Dimension  . Unsurprisingly, any Banach-Colmez space whose
. Unsurprisingly, any Banach-Colmez space whose  -dimension is positive will be disgustingly infinitely generated as a
-dimension is positive will be disgustingly infinitely generated as a 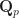 -vector space, so the Theorem really does give us an example of the desired type. Note also that Poincare duality fails in this example.
-vector space, so the Theorem really does give us an example of the desired type. Note also that Poincare duality fails in this example.
Proof. Let 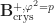 be the evident sheaf on
be the evident sheaf on 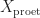 , where e.g.
, where e.g. 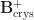 is the crystalline period sheaf defined in Tan-Tong’s paper on crystalline comparison. The key observation is that there is a short exact sequence
is the crystalline period sheaf defined in Tan-Tong’s paper on crystalline comparison. The key observation is that there is a short exact sequence
![(\ast)\;\;\; 0 \to \mathbf{V}_{LT} \to \mathbf{B}_{\mathrm{crys}}^{+,\varphi^2=p} \to \mathrm{Lie}(G)[\tfrac{1}{p}] \otimes_{\mathcal{O}_X} \widehat{\mathcal{O}}_X \to 0](https://s0.wp.com/latex.php?latex=%28%5Cast%29%5C%3B%5C%3B%5C%3B+0+%5Cto+%5Cmathbf%7BV%7D_%7BLT%7D+%5Cto%C2%A0%5Cmathbf%7BB%7D_%7B%5Cmathrm%7Bcrys%7D%7D%5E%7B%2B%2C%5Cvarphi%5E2%3Dp%7D+%5Cto+%5Cmathrm%7BLie%7D%28G%29%5B%5Ctfrac%7B1%7D%7Bp%7D%5D+%5Cotimes_%7B%5Cmathcal%7BO%7D_X%7D+%5Cwidehat%7B%5Cmathcal%7BO%7D%7D_X+%5Cto+0&bg=ffffff&fg=1a1a1a&s=0&c=20201002)
of sheaves on 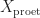 . This is a sheaf-theoretic version of the sequence (1.0.1) in Scholze-Weinstein, and it can be constructed using the methods in their paper. One can also construct it directly using the modern fancy-pants interpretation of
. This is a sheaf-theoretic version of the sequence (1.0.1) in Scholze-Weinstein, and it can be constructed using the methods in their paper. One can also construct it directly using the modern fancy-pants interpretation of  in this setup as the period domain parametrizing admissible length one modifications of the bundle
in this setup as the period domain parametrizing admissible length one modifications of the bundle  on the Fargues-Fontaine curve. (Nb. The mysterious middle term in the sequence is really the sheaf of
on the Fargues-Fontaine curve. (Nb. The mysterious middle term in the sequence is really the sheaf of  -equivariant maps from
-equivariant maps from ![H^1_{\mathrm{crys}}(G_0/W(\overline{\mathbf{F}_p}))[\tfrac{1}{p}]](https://s0.wp.com/latex.php?latex=H%5E1_%7B%5Cmathrm%7Bcrys%7D%7D%28G_0%2FW%28%5Coverline%7B%5Cmathbf%7BF%7D_p%7D%29%29%5B%5Ctfrac%7B1%7D%7Bp%7D%5D&bg=ffffff&fg=1a1a1a&s=0&c=20201002) to
to 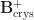 .)
.)
Anyway, this reduces us to computing the groups  and
and ![H^i_{\mathrm{proet}}(X,\mathrm{Lie}(G)[\tfrac{1}{p}] \otimes_{\mathcal{O}_X} \widehat{\mathcal{O}}_X)](https://s0.wp.com/latex.php?latex=H%5Ei_%7B%5Cmathrm%7Bproet%7D%7D%28X%2C%5Cmathrm%7BLie%7D%28G%29%5B%5Ctfrac%7B1%7D%7Bp%7D%5D+%5Cotimes_%7B%5Cmathcal%7BO%7D_X%7D+%5Cwidehat%7B%5Cmathcal%7BO%7D%7D_X%29&bg=ffffff&fg=1a1a1a&s=0&c=20201002) . This might look a bit terrifying, but it’s not so bad. In fact, the first of these can be handled by a general lemma.
. This might look a bit terrifying, but it’s not so bad. In fact, the first of these can be handled by a general lemma.
Lemma. Let 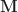 be any Banach-Colmez space over
be any Banach-Colmez space over  . For any proper rigid space
. For any proper rigid space 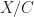 , we may regard
, we may regard 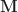 as a (pre)sheaf on
as a (pre)sheaf on 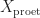 , so in particular we can talk about the pro-etale cohomology groups
, so in particular we can talk about the pro-etale cohomology groups  . In this notation, the natural map
. In this notation, the natural map 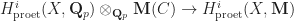 is an isomorphism.
is an isomorphism.
(Proof sketch: Use the 5 lemma to reduce to the case of effective Banach-Colmez spaces, and then to the cases of the space 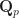 , where it’s a tautology, and the space Colmez notates
, where it’s a tautology, and the space Colmez notates  , where it follows from the primitive comparison theorem, cf. Theorem 3.17 in Scholze’s CDM survey.)
, where it follows from the primitive comparison theorem, cf. Theorem 3.17 in Scholze’s CDM survey.)
Applied to our problem, this immediately gives that 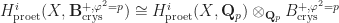 . By the standard easy computation of
. By the standard easy computation of 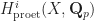 , we get that
, we get that  is a copy of
is a copy of  for either of
for either of  , and it vanishes otherwise. In particular, in degrees 0 and 2, it has Dimension
, and it vanishes otherwise. In particular, in degrees 0 and 2, it has Dimension  by some of the calculations in Colmez’s original paper.
by some of the calculations in Colmez’s original paper.
Next, we need to compute the pro-etale cohomology of ![\mathcal{E} = \mathrm{Lie}(G)[\tfrac{1}{p}] \otimes_{\mathcal{O}_X} \widehat{\mathcal{O}}_X](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BE%7D+%3D+%5Cmathrm%7BLie%7D%28G%29%5B%5Ctfrac%7B1%7D%7Bp%7D%5D+%5Cotimes_%7B%5Cmathcal%7BO%7D_X%7D+%5Cwidehat%7B%5Cmathcal%7BO%7D%7D_X&bg=ffffff&fg=1a1a1a&s=0&c=20201002) . For this, we use the fact (already in Gross and Hopkins’s original article) that
. For this, we use the fact (already in Gross and Hopkins’s original article) that ![\mathrm{Lie}(G)[\tfrac{1}{p}] \simeq \mathcal{O}_X(1)](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BLie%7D%28G%29%5B%5Ctfrac%7B1%7D%7Bp%7D%5D+%5Csimeq+%5Cmathcal%7BO%7D_X%281%29&bg=ffffff&fg=1a1a1a&s=0&c=20201002) . Let
. Let  be the evident projection of sites. Combining the description of
be the evident projection of sites. Combining the description of ![\mathrm{Lie}(G)[\tfrac{1}{p}]](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BLie%7D%28G%29%5B%5Ctfrac%7B1%7D%7Bp%7D%5D&bg=ffffff&fg=1a1a1a&s=0&c=20201002) with an easy projection formula gives an isomorphism
with an easy projection formula gives an isomorphism  . Moreover,
. Moreover,  identifies with
identifies with  in degree zero and
in degree zero and  in degree 1, and vanishes otherwise. In particular, the only nonvanishing cohomology sheaves of
in degree 1, and vanishes otherwise. In particular, the only nonvanishing cohomology sheaves of 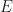 are
are 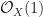 in degree 0 and
in degree 0 and 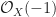 in degree 1; moreover, the latter has no global cohomology in any degree. Feeding this information into the Leray spectral sequence for
in degree 1; moreover, the latter has no global cohomology in any degree. Feeding this information into the Leray spectral sequence for 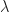 , we get that
, we get that  , so this is
, so this is 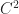 for
for  and zero otherwise.
and zero otherwise.
Finally, we can put everything together and take the long exact sequence in pro-etale cohomology associated with 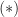 . It’s easy to check that
. It’s easy to check that  doesn’t have any global sections, and the middle term of
doesn’t have any global sections, and the middle term of 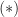 has no cohomology in degree one, so we get a short exact sequence
has no cohomology in degree one, so we get a short exact sequence  . We’ve already identified the
. We’ve already identified the  here as something of Dimension
here as something of Dimension  , so by the additivity of Dimensions in short exact sequences, we deduce that
, so by the additivity of Dimensions in short exact sequences, we deduce that  has Dimension
has Dimension  , as desired. By a similar argument, we get an isomorphism
, as desired. By a similar argument, we get an isomorphism 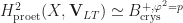 , which we already observed has Dimension
, which we already observed has Dimension  . The vanishing of all the other cohomologies of
. The vanishing of all the other cohomologies of  also follows easily.
also follows easily. 
BTW, there is nothing special about height 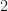 in this story; I just stuck with it for convenience. For any heght
in this story; I just stuck with it for convenience. For any heght 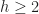 , there is an analogous rank
, there is an analogous rank 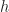
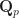 -local system
-local system  on
on  , and one can check that e.g.
, and one can check that e.g.  has Dimension
has Dimension 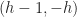 .
.
Let me briefly explain the genesis of these calculations. Several months ago Shizhang Li pointed out to me that the primitive comparison theorem doesn’t obviously generalize to 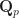 -local systems without globally defined lattices, and he also suggested that the cohomologies of
-local systems without globally defined lattices, and he also suggested that the cohomologies of  might be strange. I promptly forgot about this conversation until Monday, when Shizhang reported that Ruochuan Liu had told him in Oberwolfach several weeks ago that the Kedlaya-Liu “theorem” was false. It was then natural to double down on
might be strange. I promptly forgot about this conversation until Monday, when Shizhang reported that Ruochuan Liu had told him in Oberwolfach several weeks ago that the Kedlaya-Liu “theorem” was false. It was then natural to double down on  as a possible counterexample. Immediately after I gave a lecture on the Tan-Tong paper the next day, the sequence
as a possible counterexample. Immediately after I gave a lecture on the Tan-Tong paper the next day, the sequence 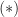 entered my head randomly. Then everything just came out. Also, luckily, we were at a restaurant with paper tablecloths.
entered my head randomly. Then everything just came out. Also, luckily, we were at a restaurant with paper tablecloths.

(I’m not sure whether Ruochuan also had this particular counterexample in mind.)
There are lots of interesting questions here, I think. Are there other natural examples of this type? Are the pro-etale cohomology groups of 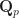 -local systems on proper rigid spaces always Banach-Colmez spaces?
-local systems on proper rigid spaces always Banach-Colmez spaces?
, the analogue of a compact complex manifold is a smooth proper rigid analytic space. In some ways, these are already surprisingly “close” to being Kahler – in particular, the Hodge-de Rham spectral sequence of such a space always degenerates at
. However, Hodge symmetry can definitely fail. A standard example is the non-archimedean Hopf surface
where
acts through diagonal multiplication. By a fun direct calculation, one checks that
and
, so Hodge symmetry fails in degree one.
satisfies (*) if it admits a formal model
over
whose special fiber is projective (as opposed to merely proper).
be a smooth proper rigid space satisfying (*). Then
.
be the complex disk, with
the punctured disk. Let
be a proper map of complex analytic spaces. Suppose that
is a submersion, and that the central fiber
is the analytification of a projective (and not necessarily smooth) algebraic variety. Then for all
with
, the fiber
satisfies Hodge symmetry and Hodge-de Rham degeneration.
is analogous to
, and
is analogous to the “nearby” fibers
with
.
