Parabolic induction is one of the most basic operations in the representation theory of p-adic groups. In the classical setting of complex coefficients, parabolic induction has a left adjoint given by the Jacquet module, and also a right adjoint given – miraculously – by the (twisted) Jacquet module for the opposite parabolic. Here all three functors are exact. One then defines supercuspidal representations as those which are killed by all Jacquet module functors, or equivalently as those which don’t occur in any parabolic induction.
With mod coefficients, parabolic induction is still exact, so it easily passes to a functor on derived categories. More precisely, fix
a p-adic reductive group, and let
be the derived category of the category of smooth
representations of
. Let
be any parabolic subgroup. Then the usual operation of parabolic induction upgrades to a t-exact functor
which preserves
. By general nonsense,
commutes with all direct sums, and hence admits a right adjoint
. Much less obviously, a recent theorem of Heyer shows that
commutes with direct products, and hence admits a left adjoint
. Moreover, Heyer also shows that
preserves
, and computes its values in some examples.
Exercise. Show that restricted to
satisfies the isomorphism
, where
is Kohlhaase’s derived duality funtor and
is the integral modulus character. Deduce that
preserves
.
Now, if you start with an irreducible representation in degree zero, it is formal that
resp.
will be concentrated in nonnegative resp. nonpositive degrees, and
of it is something explicit:
is basically the (naive) Jacquet module, and
is Emerton’s functor
of ordinary parts. In particular, when
is supersingular, both of these things vanish in degree zero. But of course, they might be nonzero in other degrees, since
and
are not t-exact.
In the special case where and
is the Borel, Heyer showed that
vanishes identically for any irreducible supersingular representation
, and the above exercise then implies that also
vanishes identically. However, if there’s one thing we’ve learned in recent years, it’s that p-adic Langlands is only simple for
– for every other group, the whole story is completely different.
Theorem (Yongquan Hu). If , there are plenty of irreducible admissible supersingular representations
such that
and
are both nonzero!
This is actually immediate from Corollary 1.2 here and basic adjunctions.
On further reflection, it is probably true that “most” supersingular representations of a given group have the property that some or
is nonzero. If you believe in some version of the mod p Langlands correspondence, this is reflected in the fact that “most” mod p Galois representations are reducible (e.g., they are Zariski-dense in the Emerton-Gee stack).
Question. Is it true that “second adjointness” holds in this setting, in the sense that as functors on on
, or even on all of
?
One can check by hand that this isomorphism is OK on irreps of using the calculations in Heyer’s paper and the exercise above. If this question has an affirmative answer, then
is necessarily concentrated in degrees
for any supersingular
, and similarly for
. In particular, in the setting of Hu’s example above, we would get that
is concentrated in degree
, and
is concentrated in degree
.
I’m not sure how ordinary parts works in the non-admissible context (the arguments in my papers, like Casselman’s original arguments, rely heavily on admissibility), but in the admisdible context I showed the top derived ordinary part is, up to a twist, the usual Jacquet module. So then the answer to your question is “yes” in the admissible context.
LikeLike
Thanks! Just to clarify, I think maybe you mean the answer is “yes” after passing to top degree cohomology on both sides.
Actually, looking more closely at your papers, and comparing with Heyer’s computation of in terms of unipotent group cohomology (Theorem B in his paper), it seems this full second adjointness question is very closely related to the question of whether “
in terms of unipotent group cohomology (Theorem B in his paper), it seems this full second adjointness question is very closely related to the question of whether “ ”.
”.
LikeLike
A further small thought. There is an obvious functor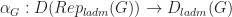 – hopefully the meaning of my notation is clear – and I think you define derived ordinary parts using the source category. In general, it feels philosophically more correct to me to work “inside”
– hopefully the meaning of my notation is clear – and I think you define derived ordinary parts using the source category. In general, it feels philosophically more correct to me to work “inside”  , so I would prefer to work with
, so I would prefer to work with  (which of course sits inside
(which of course sits inside  fully faithfully) instead of
fully faithfully) instead of  whenever possible. Although I see no reason why
whenever possible. Although I see no reason why 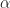 should be fully faithful in general, it still seems natural to guess that
should be fully faithful in general, it still seems natural to guess that 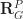 preserves the property of having locally admissible cohomology, and that
preserves the property of having locally admissible cohomology, and that  . Again, this is closely related to the second adjointness question.
. Again, this is closely related to the second adjointness question.
LikeLike
Actually, about 12 years ago I found a nice derived framework for ordinary parts and its compatibility with duality which avoids unsolved homological problems such as how notions of injective objects in various rep’n categories behave. It was explained in some talks but isn’t written up.
Not sure how it holds up in terms of contemporary developments, but I’d be happy to explain it.
LikeLike
I would love to hear about this! Feel free to write about it here, or we can switch to email if it’s easier for you, whatever you prefer.
LikeLike